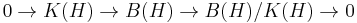Calkin algebra

In functional analysis, the Calkin algebra, named after John Wilson Calkin, is the quotient of B(H), the ring of bounded linear operators on a separable infinite-dimensional Hilbert space H, by the ideal K(H) of compact operators.

Since the compact operators is a (in fact, the only) maximal norm-closed ideal in B(H), the Calkin algebra is simple.

As a quotient of two C* algebras, the Calkin algebra is a C* algebra itself. There is a short exact sequence

0 \rightarrow K(H) \rightarrow B(H) \rightarrow B(H)/K(H) \rightarrow 0

which induces a six-term cyclic exact sequence in K-theory. Those operators in B(H) which are mapped to an invertible element of the Calkin algebra are called Fredholm operators, and their index can be described both using K-theory and directly. One can conclude, for instance, that the collection of unitary operators in the Calkin algebra are homotopy classes indexed by the integers Z. This is in contrast to B(H), where the unitary operators are path connected.

As a C* algebra, the Calkin algebra is remarkable because it is not isomorphic to an algebra of operators on a separable Hilbert space; instead, a larger Hilbert space has to be chosen (the GNS theorem says that every C* algebra is isomorphic to an algebra of operators on a Hilbert space; for many other simple C* algebras, there are explicit descriptions of such Hilbert spaces, but for the Calkin algebra, this is not the case).

The same name is now used for the analogous construction for a Banach space.

The Calkin algebra is the Corona algebra of the algebra of compact operators on a Hilbert space.

The existence of an outer automorphism of the Calkin algebra is shown to be independent of ZFC, by work of Philips and Weaver, and Farah.

References